Mathematics Department

MATHEMATICS AT GREAT MARLOW SCHOOL

The subject of mathematics aims to:

• set challenging targets
• set high expectations for all students
• offer a variety of approaches to teaching and learning to engage and motivate all students and demand their active participation
• develop mathematical literacy through correct use of mathematical vocabulary, class discussions and structured reasoning
• develop conceptual, procedural and factual fluency
• nurture resilient, independent learners who are able to use what they know to work out what they don’t know

• smooth the transition for students between key stages (including from KS2 to KS3) and ensure progression in teaching and learning throughout their time at Great Marlow School.
• maintain strong links with local leaders in maths education including Primary Maths Leads, Astra SCITT & BBO Maths Hub

• explore enrichment opportunities outside the curriculum to enhance students’ enjoyment of mathematics

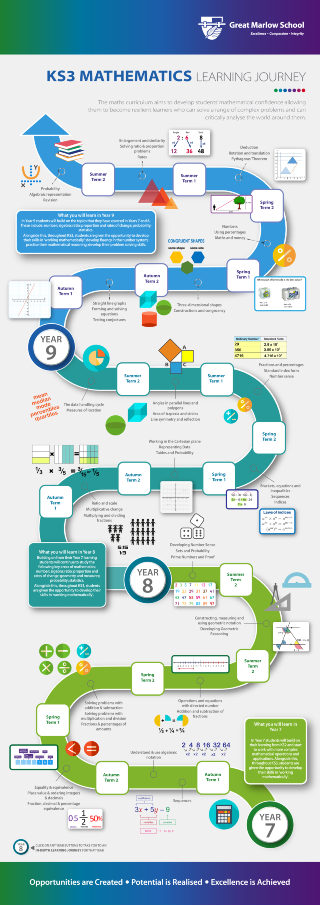
KEY STAGE 3 MATHEMATICS Year 7 

Autumn Term

The following topics are studied in the first term of the year.

• sequences
• understand and use algebraic notation
• place value and ordering integers and decimals
• fraction decimal and percentage equivalence

Spring Term

The following topics are studied in the second term of the academic year.

• solving problems with addition and subtraction
• solving problems with multiplication and division
• fractions and percentages of amounts
• operations and equations with directed number
• addition and subtraction of fractions

Summer Term

These are the topics studied in the third term of the academic year.

• constructing, measuring and using geometric notation
• developing geometric reasoning
• developing number sense
• sets and probability
• prime numbers and proof

KEY STAGE 3 MATHEMATICS Year 8 

Autumn Term

The topics that follow are studied in the first term of Year 8.

• ratio and scale
• multiplicative change
• multiplying and dividing fractions
• working the cartesian plane
• representing data
• tables and probability

Spring Term

The topics taught in the second term of Year 8 are as follows.

• brackets equations and inequalities
• sequences
• indices
• fractions and percentages
• standard index form
• number sense

Summer Term

In the summer term of Year 8 these topics are taught.

• angles in parallel lines and polygons
• area of trapezia and circles
• line symmetry and reflection
• the data handing cycle
• measures of location

KEY STAGE 3 MATHEMATICS Year 9 

Autumn Term

The following topics are studied in the first term of the year.

• fractions and decimals
• averages
• area of 2D shapes
• 3D shapes
• algebraic expressions
• ratio and proportion

Spring Term

The following topics are studied in the second term of the academic year.

• linear graphs
• representing data
• angles
• collecting data

Summer  Term

These are the topics studied in the third term of the academic year.

• transformations
• solving equations
• scatter graphs
• constructions
• Pythagoras’ theorem

KEY STAGE 4 MATHEMATICS Year 10 (Middle Sets)  

Edexcel Foundation GCSE in Mathematics

Autumn Term

Number

• Calculations: use priority of operations with positive and negative numbers; simplify calculations by cancelling; use inverse operations.
• Decimal Numbers: round to a given number of decimal place; multiply and divide decimal numbers.
• Place Value: write decimal numbers of millions; round to a given number of significant figures; estimate answers to calculations; use one calculation to find the answer to another.
• Factors and Multiples: recognise 2-digit prime numbers; find factors and multiples of numbers; find common factors and common multiples of two numbers; find the HCF and LCM of two numbers by listing.
• Squares, Cubes and Roots: find square roots and cube roots; recognise powers of 2, 3, 4 and 5; understand surd notation on a calculator.
• Index Notation: find square roots and cube roots; recognise powers of 2, 3, 4 and 5; understand surd notation on a calculator.
• Prime Factors: write a number as the product of its prime factors; use prime factor decomposition and Venn diagrams to find the HCF and LCM.

Graphs, Tables and Charts

• Frequency Tables: designing tables and data collection sheets; reading data from tables.
• Two-Way Tables: use data from tables; design and use two-way tables.
• Representing Data: draw and interpret comparative and composite bar charts; interpret and compare data shown in bar charts, line graphs and histograms.
• Time Series: plot and interpret time series graphs; use trends to predict what might happen in the future.
• Stem and Leaf Diagrams: construct and interpret stem and leaf and back-to-back stem and leaf diagrams.
• Pie Charts: draw and interpret pie charts.
• Scatter Graphs: plot and interpret scatter graphs; determine whether or not there is a relationship between sets of data.
• Line of Best Fit: draw a line of best fit on a scatter graph; use the line of best fit to predict values.

Fractions and Percentages

• Working with Fractions: compare fractions; add and subtract fractions; use fractions to solve problems.
• Operations with Fractions: find a fraction of a quantity or measurement; use fractions to solve problems.
• Multiplying Fractions: multiply whole numbers, fractions and mixed numbers; simplify calculations by cancelling.
• Dividing Fractions: divide a whole number by a fraction; divide a fraction by a whole number or a fraction.
• Fractions and Decimals: convert fractions to decimals and vice versa; use decimals to find quantities; write one number as a fraction of another.
• Fractions and Percentages: convert percentages to fractions and vice versa; write one number as a percentage of another.
• Calculating Percentages 1: convert percentages to decimals and vice versa; find a percentage of a quantity; use percentages to solve problems; calculate simple interest.
• Calculating Percentages 2: calculate percentage increases and decreases; use percentages in real-life situations; calculate VAT (value added tax).

Equations, Inequalities and Sequences

• Solving Equations 1: understand and use inverse equations; rearrange simple linear equations; solve simple linear equations.
• Solving Equations 2: solve two-step equations.
• Solving Equations with Brackets: solve linear equations with brackets; solve equations with unknowns on both sides.
• Introducing Inequalities: use correct notation to show inclusive and exclusive inequalities; solve simple linear inequalities; write down whole numbers which satisfy an inequality; represent inequalities on a number line.
• More Inequalities: solve two-sided inequalities.
• More Formulae: substitute values into formulae and solve equations; change the subject of a formula; know the difference between an expression, an equation, a formula and an identity.
• Generating Sequences: recognise and extend sequences.
• Using the Nth Term of a Sequence: use the nth term to generate terms of a sequence; find the nth term of an arithmetic sequence.

Spring Term

Angles 

Averages and Range

• Mean and Range: calculate the mean from a list and from a frequency table; compare sets of data using the mean and range.
• Mode, Median and Range: find the mode, median and range from a stem and leaf diagram; identify outliers; estimate the range from a grouped frequency table.
• Types of Average: recognise the advantages and disadvantages of each type of average; find the modal class; find the median from a frequency table.
• Estimating the Mean: estimate the mean of grouped data.
• Sampling: understand the need for sampling; understand how to avoid bias.

Perimeter, Area and Volume 1 

• Rectangles, Parallelograms and Triangles: calculate the perimeter and area of rectangles, parallelograms and triangles; estimate lengths, areas and costs; calculate a missing length, given the area.
• Trapezia and Changing Units: calculate the area and perimeter of trapezia; find the height of a trapezium given its area; convert between area measures.
• Area of Compound Shapes: calculate the perimeter and area of shapes made from triangles and rectangles; calculate areas in hectares, and convert between ha and m2.
• Surface Area of 3D Solids: calculate the surface area of a cuboid; calculate the surface area of a prism.
• Volume of Prisms: calculate the volume of a cuboid; calculate the volume of a prism.
• More Volume and Surface Area: solve problems involving surface area and volume; convert between measures of volume.

     Graphs

• Coordinates: find the midpoint of a line segment; recognise, name and plot straight-line graphs parallel to the axes.
• Linear Graphs: generate and plot coordinates from a rule; plot straight-line graphs from tables of values; draw graphs to represent relationships.
• Gradient: find the gradient of a line; identify and interpret the gradient from an equation; understand that parallel lines have the same gradient.
• Y = Mx + C: understand what m and c represent in y = mx + c; find the equations of straight-line graphs; sketch graphs given the values of m and c.
• Real-Life Graphs: draw and interpret graphs from real data.
• Distance-Time Graphs: use distance–time graphs to solve problems; draw distance–time graphs; interpret rate of change graphs.
• More Real-Life Graphs: draw and interpret a range of graphs; understand when predictions are reliable.

Transformations

• Translation: translate a shape on a coordinate grid; use a column vector to describe a translation.
• Reflection: draw a reflection of a shape in a mirror line; draw reflections on a coordinate grid; describe reflections on a coordinate grid.
• Rotation: rotate a shape on a coordinate grid; describe a rotation.
• Enlargement: enlarge a shape by a scale factor; enlarge a shape using a centre of enlargement.
• Describing Enlargements: identify the scale factor of an enlargement; find the centre of enlargement; describe an enlargement.
• Combining Transformations: transform shapes using more than one transformation; describe combined transformations of shapes on a grid.

Summer Term

Ratio and Proportion

• Writing Ratios: use ratio notation; write a ratio in its simplest form; solve problems using ratios.
• Using Ratios 1: solve simple problems using ratios.
• Ratios and Measures: use ratios to convert between units; write and use ratios for shapes and their enlargements.
• Using Ratios 2: divide a quantity into 2 parts in a given ratio; divide a quantity into 3 parts in a given ratio; solve word problems using ratios.
• Comparing Using Ratios: use ratios involving decimals; compare ratios; solve ratio and proportion problems.
• Using Proportion: use the unitary method to solve proportion problems; solve proportion problems in words; work out which product is better value for money.
• Proportion and Graphs: recognise and use direct proportion on a graph; understand the link between the unit ratio and the gradient.
• Proportion Problems: recognise different types of proportion; solve word problems involving direct and inverse proportion.

Right-Angled Triangles 

• Pythagoras’ Theorem 1: understand Pythagoras’ theorem; calculate the length of the hypotenuse in a right-angled triangle; solve problems using Pythagoras’ theorem.
• Pythagoras’ Theorem 2: calculate the length of a line segment ab; calculate the length of a shorter side in a right-angled triangle.
• Trigonometry: The Sine Ratio 1: understand and recall the sine ratio in right-angled triangles; use the sine ratio to calculate the length of a side in a right-angled triangle; use the sine ratio to solve problems.
• Trigonometry: The Sine Ratio 2: use the sine ratio to calculate an angle in a right-angled triangle; use the sine ratio to solve problems.
• Trigonometry: The Cosine Ratio: understand and recall the cosine ratio in right-angled triangles; use the cosine ratio to calculate the length of a side in a right-angled triangle; use the cosine ratio to calculate an angle in a right-angled triangle; use the cosine ratio to solve problems.
• Trigonometry: The Tangent Ratio: understand and recall the tangent ratio in right-angled triangles; use the tangent ratio to calculate the length of a side in a right-angle triangle; use the tangent ratio to calculate an angle in a right-angled triangle; solve problems using an angle of elevation or depression.
• Finding Lengths and Angles Using Trigonometry : understand and recall trigonometric ratios in right-angled triangles; use trigonometric ratios to solve problems; know the exact values of the sine, cosine and tangent of some angles.

Probability

• Calculating Probability: calculate simple probabilities from equally likely events; understand mutually exclusive and exhaustive outcomes.
• Two Events: use two-way tables to record the outcomes from two events; work out probabilities from sample space diagrams.
• Experimental Probability: find and interpret probabilities based on experimental data; make predictions from experimental data.
• Venn Diagrams: use Venn diagrams to work out probabilities; understand the language of sets and Venn diagrams.
• Tree Diagrams: use frequency trees and tree diagrams; work out probabilities using tree diagrams; understand independent events.
• More Tree Diagrams: understand when events are not independent; solve probability problems involving events that are not independent.

Multiplicative Reasoning 

• Percentages: calculate a percentage profit or loss; express a given number as a percentage of another in more complex situations; find the original amount given the final amount after a percentage increase or decrease
• Growth and Decay: find an amount after repeated percentage change; solve growth and decay problems.
• Compound Measures: solve problems involving compound measures.
• Distance, Speed and Time: convert between metric speed measures; calculate average speed, distance and time; use formulae to calculate speed and acceleration.
• Direct and Inverse Proportion: use ratio and proportion in measures and conversions; use inverse proportions.

Constructions, Loci and Bearings

• 3D Solids: recognise 3D shapes and their properties; describe 3D shapes using the correct mathematical words; understand the 2D shapes that make up 3D objects.
• Plans and Elevations: identify and sketch planes of symmetry of 3D shapes; understand and draw plans and elevations of 3D shapes; sketch 3D shapes based on their plans and elevations.
• Accurate Drawings 1: make accurate drawings of triangles using a ruler, protractor and compasses; identify SSS, ASA, SAS and RHS triangles as unique from a given description; identify congruent triangles
• Scale Drawings and Maps: draw diagrams to scale; correctly interpret scales in real-life contexts; use scales on maps and diagrams to work out lengths and distances; know when to use exact measurements and estimations on scale drawings and maps; draw lengths and distances correctly on given scale drawings.
• Accurate Drawings 2: accurately draw angles and 2D shapes using a ruler, protractor and compasses; construct a polygon inside a circle; recognise nets and make accurate drawings of nets of common 3D objects.
• Constructions: draw accurately using rulers and compasses; bisect angles and lines using rulers and compasses.
• Loci and Regions: draw loci for the path of points that follow a given rule; identify regions bounded by loci to solve practical problems.
• Bearings: find and use three-figure bearings; use angles at parallel lines to work out bearings; solve problems involving bearings and scale diagrams.

KEY STAGE 4 MATHEMATICS Year 10 (Higher Paper) 

Edexcel Higher GCSE in Mathematics

Autumn Term

 Number

• Number Problems and Reasoning: work out the total number of ways of performing a series of tasks.
• Place Value and Estimating: estimate an answer; use place value to answer questions.
• HCF and LCM: write a number of the product of its prime factors; find the HCF and LCD of two numbers.
• Calculating with Powers (Indices): use powers and roots in calculations; multiply and divide using index laws; work out a power raised to a power.
• Zero, Negative and Fractional Indices: use negative indices; use fractional indices.
• Powers of 10 and Standard Form: write a number in standard form; calculate with numbers in standard form.
• Surds: understand the difference between rational and irrational numbers; simplify a surd; rationalise a denominator.

Algebra Interpreting and Representing Data

• Statistical Diagrams 1: construct and use back-to-back stem and leaf diagrams; construct and use frequency polygons and pie charts.
• Time Series: plot and interpret time series graphs; use trends to predict what might happen in the future.
• Scatter Graphs: plot and interpret scatter graphs; determine whether or not there is a linear relationship between two variables.
• Line of Best Fit: draw a line of best fit on a scatter graph; use the line of best fit to predict values.
• Averages and Range: decide which average is best for a set of data; estimate the mean and range from a grouped frequency table; find the modal class and the group containing the median.
• Statistical Diagrams 2: construct and use two-way tables; choose appropriate diagrams to display data; recognise misleading graphs.

Fractions, Ratio and Percentages

• Fractions: add, subtract, multiply and divide fractions and mixed numbers; find the reciprocal of an integer, decimal or fraction.
• Ratios: write ratios in the form 1 : n or n : 1; compare ratios; find quantities using ratios; solve problems involving ratios.
• Ratio and Proportion: convert between currencies and measures; recognise and use direct proportion; solve problems involving ratios and proportion.
• Percentages: work out percentage increases and decreases; solve real-life problems involving percentages.
• Fractions, Decimals and Percentages: work out percentage increases and decreases; solve real-life problems involving percentages.

Angles and Trigonometry

• Angle Properties of Triangles and Quadrilaterals: derive and use the sum of angles in a triangle and in a quadrilateral; derive and use the fact that the exterior angle of a triangle is equal to the sum of the two opposite interior angles.
• Interior Angles of a Polygon: calculate the sum of the interior angles of a polygon; use the interior angles of polygons to solve problems.
• Exterior Angles of a Polygon: know the sum of the exterior angles of a polygon; use the angles of polygons to solve problems.
• Pythagoras’ Theorem 1: calculate the length of the hypotenuse in a right-angled triangle; solve problems using Pythagoras’ theorem; calculate the length of a shorter side in a right-angled triangle.
• Trigonometry 1: use trigonometric ratios to find lengths in a right-angled triangle; use trigonometric ratios to solve problems; use trigonometric ratios to calculate an angle in a right-angled triangle; find angles of elevation and angles of depression; use trigonometric ratios to solve problems; know the exact values of the sine, cosine and tangent of some angles.

Spring Term

Graphs

Area and Volume

• Perimeter and Area: find the perimeter and area of compound shapes; recall and use the formula for the area of a trapezium.
• Units and Accuracy: convert between metric units of area; calculate the maximum and minimum possible values of a measurement.
• Prisms: convert between metric units of volume; calculate volumes and surface areas of prisms.
• Circles: calculate the area and circumference of a circle; calculate area and circumference in terms of π.
• Sectors of Circles: calculate the perimeter and area of semicircles and quarter circles; calculate arc lengths, angles and areas of sectors of circles.
• Cylinders and Spheres: calculate volume and surface area of a cylinder and a sphere; solve problems involving volumes and surface areas.
• Pyramids and Cones: calculate volume and surface area of pyramids and cones; solve problems involving pyramids and cones.
• Transformations and Constructions
• 3D Solids: draw plans and elevations of 3d solids.
• Reflection and Rotation: reflect a 2D shape in a mirror line; rotate a 2D shape about a centre of rotation; describe reflections and rotations.
• Enlargement: enlarge shapes by fractional and negative scale factors about a centre of enlargement.
• Transformations and Combinations of Transformations: translate a shape using a vector; carry out and describe combinations of transformations.
• Bearings and Scale Drawings: draw and use scales on maps and scale drawings; solve problems involving bearings.
• Constructions 1: construct triangles using a ruler and compasses; construct the perpendicular bisector of a line; construct the shortest distance from a point to a line using a ruler and compasses.
• Constructions 2: bisect an angle using a ruler and compasses; construct angles using a ruler and compasses; construct shapes made from triangles using a ruler and compasses.
• Loci: draw a locus; use loci to solve problems.

Equations and Inequalities

• Solving Quadratic Equations 1: find the roots of quadratic functions; rearrange and solve simple quadratic equations.
• Solving Quadratic Equations 2: solve more complex quadratic equations; use the quadratic formula to solve a quadratic equation.
• Completing the Square: complete the square for a quadratic expression; solve quadratic equations by completing the square.
• Solving Simple Simultaneous Equations: solve simple simultaneous equations; solve simultaneous equations for real-life situations.
• More Simultaneous Equations: use simultaneous equations to find the equation of a straight line; solve linear simultaneous equations where both equations are multiplied; interpret real-life situations involving two unknowns and solve them.
• Solving Linear and Quadratic Simultaneous Equations: solve simultaneous equations with one quadratic equation; use real-life situations to construct quadratic and linear equations and solve them.
• Solving Linear Inequalities: solve inequalities and show the solution on a number line and using set notation.

Probability

• Combined Events: use the product rule for finding the number of outcomes for two or more events; list all the possible outcomes of two events in a sample space diagram.
• Mutually Exclusive Events: identify mutually exclusive outcomes and events; find the probabilities of mutually exclusive outcomes and events; find the probability of an event not happening.
• Experimental Probability: work out the expected results for experimental and theoretical probabilities; compare real results with theoretical expected values to see if a game is fair
• Independent Events and Tree Diagrams: draw and use frequency trees; calculate probabilities of repeated events; draw and use probability tree diagrams.
• Conditional Probability: decide if two events are independent; draw and use tree diagrams to calculate conditional probability; draw and use tree diagrams without replacement; use two-way tables to calculate conditional probability.
• Venn Diagrams and Set Notation: use Venn diagrams to calculate conditional probability; use set notation.

Summer Term

Multiplicative Reasoning

• Growth and Decay: find an amount after repeated percentage changes; solve growth and decay problems.
• Compound Measures: calculate rates; convert between metric speed measures; use a formula to calculate speed and acceleration.
• More Compound Measures: solve problems involving compound measures.
• Ratio and Proportion: use relationships involving ratio; use direct and indirect proportion.
• Similarity and Congruence
• Congruence: show that two triangles are congruent; know the conditions of congruence.
• Geometric Proof and Congruence: prove shapes are congruent; solve problems involving congruence.
• Similarity: use the ratio of corresponding sides to work out scale factors; find missing lengths on similar shapes; use similar triangles to work out lengths in real life; use the link between linear scale factor and area scale factor to solve problems.
• Similarity in 3D Solids: use the link between scale factors for length, area and volume to solve problems.

More Trigonometry

• Accuracy: understand and use upper and lower bounds in calculations involving trigonometry.
• Graph of The Sine Function: understand how to find the sine of any angle know the graph of the sine function and use it to solve equations.
• Graph of The Cosine Function: understand how to find the cosine of any angle; know the graph of the cosine function and use it to solve equations.
• The Tangent Function: understand how to find the tangent of any angle; know the graph of the tangent function and use it to solve equations.
• Calculating Areas and The Sine Rule: find the area of a triangle and a segment of a circle; use the sine rule to solve 2D problems.
• The Cosine Rule and 2D Trigonometric Problems: use the cosine rule to solve 2d problems; solve bearings problems using trigonometry.
• Solving Problems in 3D: use Pythagoras’ theorem in 3D; use trigonometry in 3D.
• Transforming Trigonometric Graphs: recognise how changes in a function affect trigonometric graphs.

Further Statistics

• Sampling: understand how to take a simple random sample; understand how to take a stratified sample.
• Cumulative Frequency: draw and interpret cumulative frequency tables and diagrams; work out the median, quartiles and interquartile range from a cumulative frequency diagram.
• Box Plots: find the quartiles and the interquartile range from stem-and-leaf diagrams; draw and interpret box plots.
• Drawing Histograms: understand frequency density; draw histograms.
• Interpreting Histograms: interpret histograms.
• Comparing and Describing Populations: compare two sets of data.

Equations and Graphs

• Solving Simultaneous Equations Graphically: solve simultaneous equations graphically.
• Representing Inequalities Graphically: represent inequalities on graphs; interpret graphs of inequalities.
• Graphs of Quadratic Functions: recognise and draw quadratic functions.
• Solving Quadratic Equations Graphically: find approximate solutions to quadratic equations graphically; solve quadratic equations using an iterative process.
• Graphs of Cubic Functions: find the roots of cubic equations; sketch graphs of cubic functions; solve cubic equations using an iterative process.

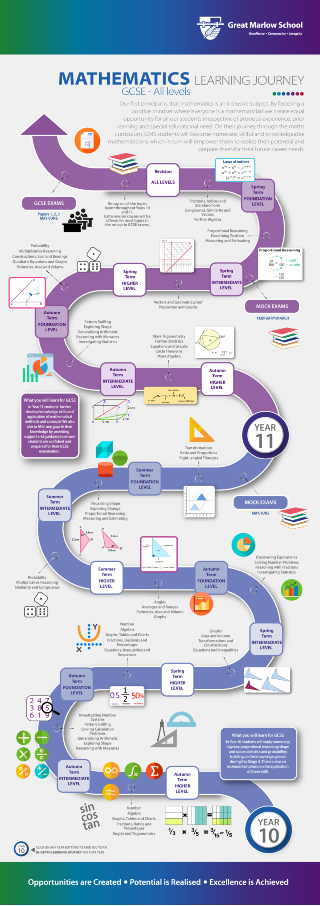
KEY STAGE 4 MATHEMATICS Year 11  (Foundation Paper) 

Edexcel Foundation GCSE in Mathematics

Autumn Term

Quadratic Equations and Graphs

Perimeter, Area and Volume 2

• Circumference of a Circle 1: calculate the circumference of a circle; solve problems involving the circumference of a circle; calculate the circumference and radius of a circle; nwork out percentage error intervals.
• Area of a Circle: work out the area of a circle; work out the radius or diameter of a circle; solve problems involving the area of a circle; give answers in terms of π.
• Semicircles and Sectors: understand and use maths language for circles and perimeters; work out areas of semicircles and quarter circle and perimeters; solve problems involving sectors of circles.
• Composite 2D Shapes and Cylinders: solve problems involving areas and perimeters of 2D shapes; work out the volume and surface area of cylinders.
• Pyramids and Cones: work out the volume of a pyramid; work out the surface area of a pyramid; work out the volume of a cone; work out the surface area of a cone.
• Spheres and Composite Solids: work out the volume of a sphere; work out the surface area of a sphere; work out the volume and surface area of composite solids.

Fractions, Indices and Standard Form

• Multiplying and Dividing Fractions: multiply and divide mixed numbers and fractions.
• The Laws of Indices: to know and use the laws of indices.
• Writing Large Numbers in Standard Form: write large numbers in standard form; convert large numbers from standard form into ordinary numbers.
• Writing Small Numbers in Standard Form: write small numbers in standard form; convert numbers from standard form with negative powers of ordinary numbers
• Calculating with Standard Form: to multiply and divide numbers in standard form; to add and subtract numbers in standard form.

Congruence, Similarity And Vectors

• Similarity and Enlargement: understand similarity; use similarity to solve angle problems.
• More Similarity: find the scale factor of an enlargement; use similarity to solve problems.
• Using Similarity: understand the similarity of regular polygons; calculate perimeters of similar shapes.
• Congruence: recognise congruent shapes; use congruence to work out unknown angles; use congruence to work out unknown sides.
• Vectors: add and subtract vectors; find the resultant of two vectors; subtract vectors; find multiples of a vector.

More Algebra

• Graphs of Cubic and Reciprocal Functions: draw and interpret graphs of cubic functions; draw and interpret graphs of y = 1/x.
• Non-Linear Graphs: draw and interpret non-linear graphs to solve problems.
• Solving Simultaneous Equations Graphically: solve simultaneous equations by drawing a graph; write and solve simultaneous equations.
• Solving Simultaneous Equations Algebraically: solve simultaneous equations algebraically.
• Rearranging Formulae: change the subject of a formula.
• Proof: identify expressions, equations, formulae and identities; prove results using algebra.

Spring and Summer Terms

• Revision Schedule Followed

KEY STAGE 4 MATHEMATICS Year 11  (Higher Paper) 

Edexcel Higher GCSE in Mathematics

Autumn Term

Circle Theorems

• Radii and Chords: solve problems involving angles, triangles and circles; understand and use facts about chords and their distance from the centre of a circle; solve problems involving chords and radii.
• Tangents: understand and use facts about tangents at a point and from a point; give reasons for angle and length calculations involving tangents.
• Angles in Circles 1: understand, prove and use facts about angles subtended at the centre and the circumference of circles; understand, prove and use facts about the angle in a semicircle being a right angle; find missing angles using these theorems and give reasons for answers.
• Angles in Circles 2: understand, prove and use facts about angles subtended at the circumference of a circle; understand, prove and use facts about cyclic quadrilaterals; prove the alternate segment theorem.
• Applying Circle Theorems: solve angle problems using circle theorems; give reasons for angle sizes using mathematical language find the equation of the tangent to a circle at a given point.

More Algebra

• Rearranging Formulae: change the subject of a formula where the power of the subject appears; change the subject of a formula where the subject appears twice.
• Algebraic Fractions: add and subtract algebraic fractions; multiply and divide algebraic fractions; change the subject of a formula involving fractions where all the variables are in the denominators.
• Simplifying Algebraic Fractions: simplify algebraic fractions.
• More Algebraic Fractions: add and subtract more complex algebraic fractions; multiply and divide more complex algebraic fractions.
• Surds: simplify expressions involving surds; expand expressions involving surds; rationalise the denominator of a fraction.
• Solving Algebraic Fraction Equations: solve equations that involve algebraic fractions.
• Functions: use function notation; find composite functions; find inverse functions.
• Proof: prove a result using algebra.

Vectors and Geometric Proof

• Vectors and Vector Notation: understand and use vector notation; work out the magnitude of a vector.
• Vector Arithmetic: calculate using vectors and represent the solutions graphically; calculate the resultant of two vectors.
• More Vector Arithmetic: solve problems using vectors; use the resultant of two vectors to solve vector problems.
• Parallel Vectors and Collinear Points: express points as position vectors; prove lines are parallel; prove points are collinear.
• Solving Geometric Problems: solve geometric problems in two dimensions using vector methods; apply vector methods for simple geometric proofs.

Proportion and Graphs

• Direct Proportion: write and use equations to solve problems involving direct proportion.
• More Direct Proportion: write and use equations to solve problems involving direct proportion; solve problems involving square and cubic proportionality.
• Inverse Proportion: write and use equations to solve problems involving inverse proportion; use and recognise graphs showing inverse proportion.
• Exponential Functions: recognise graphs of exponential functions; sketch graphs of exponential functions.
• Non-Linear Graphs: calculate the gradient of a tangent at a point; estimate the area under a non-linear graph.
• Translating Graphs of Functions: understand the relationship between translating a graph and the change in its function notation.
• Reflecting and Stretching Graphs of Functions: understand the effect stretching a curve parallel to one of the axes has on its function form; understand the effect reflecting a curve in one of the axes has on its function form.

Spring and Summer Terms

• Revision Schedule Followed

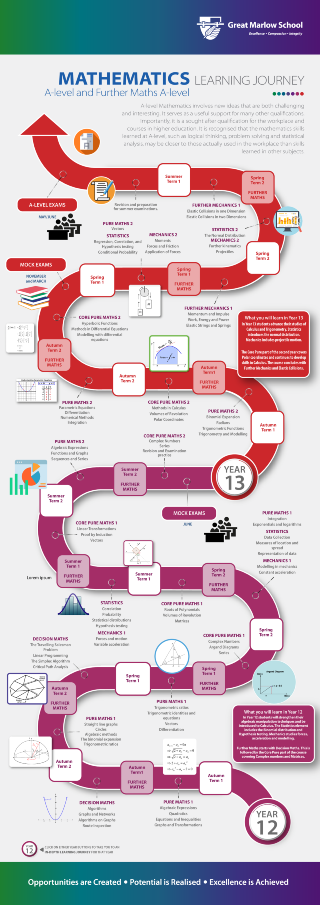
Key Stage 5 Mathematics

Students will study the new AQA A-level Mathematics specification. This is a full two year A-level course. The new A-level provides students with a thorough grounding in the mathematical tools and techniques often needed in the workplace. The logic and reasoning skills developed by studying A-level Mathematics serves as a useful support for many other qualifications. Importantly it is a sought after qualification for the workplace and courses in higher education.

It is recognised that the mathematics skills learned at A-level, such as logical thinking, problem solving and statistical analysis, may be closer to those actually used in the workplace than skills learned in other subjects.

The Mathematics Department has a team of experienced teachers. Students are taught in small groups where the subject matter can be discussed in detail in seminar type lessons that complement the more traditional form of lesson. Homework is set regularly; it comprises undertaking additional tasks that stretch the understanding of the subject.

Edexcel A-level Mathematics: 9MA0

Course Content

This is a two year course and students will sit the whole assessment in May and June in the second year of study. At the end of the first year of study there is an internally set examination, to assess progress.

While studying mathematics students will:

• use mathematical skills and knowledge to solve problems
• use mathematics, in real life situations, to show what is happening and what might happen in different circumstances
• use graphics calculators and other resources effectively and by doing so will understand their limitations and when it is appropriate to use such technology
• solve quite complicated problems by using mathematical arguments and logic

The course is divided into units, which cover three of the branches of mathematics. Students will study:

Pure Mathematics, Statistics and Mechanics

There are three externally examined papers. 9MA0/01, 9MA0/02 and 9MA0/03

Papers 1 and 2 examine the Pure Mathematics elements, including:

proof, algebra and functions, coordinate geometry in the (x,y) plane, sequences and series, trigonometry, exponentials and logarithms, differentiation, integration, and vectors.

The knowledge required for Paper 1 is assumed knowledge for Paper 2 and may be tested within parts of questions.

Paper 3 covers the applied elements,

Section A covers the statistics elements, including:

statistical sampling, data presentation and interpretation, probability, statistical distributions, and statistical hypothesis testing.

Section B covers the mechanics elements, including:

quantities and units in mechanics, kinematics, forces and Newton’s laws, and moments.

Each paper is 2 hours long and provides 33.33% of the qualification.

Calculators can be used in all three papers.

Entry requirements

Students who have achieved a good Grade 7 from the Higher GCSE paper will be eligible to study Mathematics at A- level.